සංඛ්යාන විද්යාව පිළිබඳ මේ ලිපි පෙළ ලිවීමේ දී බී.එෆ්. ස්කිනර විසින් හඳුන්වා දුන් පියවර පාඩම් ක්රමය (programmed learning) ද භාවිත කරනු ලැබේ. එහි දී ඔබේ අවබෝධය තහවුරු කිරීම සඳහා හිස්තැන් පිරවීමේ ප්රශ්න ලිපියට ඇතුළත් කරඇත.
කයි වර්ග පරික්ෂාව Chi squire test
පර්යේෂණයක දී දත්ත රැස් කරන විට ලැබෙන අගයයන් සහ එම පර්යේෂණයේ දී පර්යේෂක බලාපොරොත්තු වන අගයයන්, අතර වෙනසක් තිබේන්නට පුළුවන. එම වෙනස අහම්බෙන් වූ වෙනසක් ද නැත හොත් වෙසෙසි වෙනසක් ද යන්න නිශ්චය කර ගැනීමට කරනු ලබන පරීක්ෂාව කයි-වර්ග පරීක්ෂාව යනුවෙන් හැදින්වේ.
සාමාන්යයෙන් පර්යේෂණයක දී නිරීක්ෂිත අගයයන්, එම පර්යේෂණයේ දී පර්යේෂක අපේක්ෂා කරන අගයයන්ට සර්වසම නො වේ. එම අගයයන් අතර යම් කිසි වෙනසක් පවතී. මෙම වෙනස සැලකිය යුතු තරමේ වෙනසක් දැයි දැනගැනීමට කයි-වර්ග පරීක්ෂාව වැදගත් වේ. සාමාන්ය භාවිතයේ දී සැලකිය යුතු තරමේ වෙනසක් යන්න සංඛ්යානයේ දී හැදින්වෙනුයේ වෙසෙසි වෙනසක් (Significant difference) යනුවෙනි. නිරීක්ෂිත හා අපේක්ෂිත අගයයන් අතර ඇති එම වෙනස සැලකිය යුතු තරමේ වෙනසක් නො වේ නම් එම වෙනස ස්වභාවයෙන් ඇති විචලතාව නිසා ඇතිවන්නකි. එනම් එම වෙනස සම්භාවනාව (Chance) හෙවත් අහම්බය නිසා ඇති වන වෙනසකි.
අපි පළමු ව පර්යේෂණයක දී ඒකල නියැදි ස`දහා කයිවර්ග පරීක්ෂාව භාවිත කරන අයුරු විමසමු. පර්යේෂණයක දී භාවිත කරනු ලබන ඒකල නියැදියක් ස`දහා උදාහරණයක් නම් ,ඔබ අධ්යාපනික ග්රන්ථ කියැවීමට කැමති ද?, යන ප්රශ්නයට ඔව් හෝ නැති ලෙස පිළිතුරු ලැබෙන සේ 11 වන ශ්රේණියේ ළමයින් පිළිතුරු දුන් විට, එම ළමයින් කණ්ඩායමයි. මීට හේතුව මෙහි දී එක් නියැදියක් පමණක් තිබීමයි.
සංගහනය
දත්ත රැස් කිරීමට අදාළ වූ විෂයාංක සමුහයයි. උදා÷ ආයතනයක සේවය කරන සේවකයන්ගේ නිවාඩු පිළිබඳ ව අධ්යයනය කිරීමට අවශ්ය වූ විට ආයතනයේ සිටින සියලූ ම සේවකයින් එහි සංගහනය වේ.
නියැදිය
සංගහනය ඉතා විශාල වූ විට එහි හැම විෂයාංකයක් ම පරීක්ෂා කිරිම අසීරු වන නිසා සංගහනයේ කොටසක් පමණක් පර්යේෂණයට භාජනය කරයි. එසේ සංගහනයෙන් තෝරා ගන්නා කොටස නියැදිය නම් වේ.
උදා:- ශ්රී ලංකාවේ ළමයින්ගේ අධ්යාපනික තත්ත්වය පිළිබඳ සොයා බැලීමට අවශ්ය වූ විට සිටින සියලූ ම ළමයින් පර්යේෂණයට භාජනය කිරීම අපහසු නිසා තෝරා ගත් ළමයින් කොටසක් පමණක් පරීක්ෂණයට භාජනය කරයි. එසේ තෝරා ගත් ළමයින් කොටස නියැදිය නම් වේ.
නිරීක්ෂිත සංඛ්යාත සහ අපේක්ෂිත සංඛ්යාත
මෙතෙක් පැවසූ කරුණු අනුව, නියැදි භාවිතයෙන් ලැබෙන ප්රතිඵල, සම්භාවිතාව යන සංකල්පය අනුව, අපේක්ෂිත ෙසෙද්ධාන්තික ප්රතිඵල සමග සෑම විට ම සැසදෙන්නේ නැත. එවැනි අවස්ථාවල දී නිරීක්ෂිත සංඛ්යාත, අපේක්ෂිත සංඛ්යාතවලින් වෙනස් වන්නේ කෙසේදැයි තීරණය කර ගැනීමට කයි වර්ග පරික්ෂාව (ං2* භාවිත කරනු ලැබේ.
උදාහරණයක් ලෙස කාසියක් සිය වරක් උඩ දමයි. මෙහි දි ෙසෙද්ධාන්තික වශයෙන් සැලකීමේ දි 50 වරක් සිරසත් 50 වරක් අගයත් වැටීම අපේක්ෂා කරයි. එනම් අපේක්ෂිත සංඛ්යාත වනුයේ
“සිරස” වැටීම ‐ 50
“අගය වැටීම” ‐ 50
එහෙත් එලෙස අපේක්ෂිත අගය සමාන ව ලැබෙන්නේ කලාතුරකිනි. මෙහි දි සත්ය වශයෙන් අපේක්ෂිත අගය ලෙස ලැබුණේ
සිරස – 30 වාරයක්
අගය – 70 වාරයක් වේ යයි සිතමු.
ඒ අනුව සත්ය වශයෙන් නිරීක්ෂණය කිරිමෙන් ලැබෙන නිරීක්ෂිත සංඛ්යාත වනුයේ
“සිරස” වැටීම ‐ 30
“අගය” වැටීම‐ 70 වේ.
මෙවිට සිරස වැටීම පිළිබඳ අපෙක්ෂිත වූ සම-සම අගය, 30-70 ලෙස වෙනස් වී ඇත. මේ වෙනස වෙසෙසි ද යනු පිරික්සීමට කයි වර්ග පරීක්සාව භාවිත කළ හැකි ය.
කයි වර්ග පරික්ෂාව කරන ආකාරය
1 වන උදාහරණය:- සිසුන් 80කගේ අධ්යාපනික ග්රන්ථ කියවීමේ කැමැත්ත පිළිබඳ පර්යේෂණයක දී ලබා දුන් ප්රශ්නාවලියක අඩංගු වූ ප්රශ්නයකට ලද ප්රතිචාර අනුව ලබා ගත් දත්ත පහත දැක්වෙයි.
ප්රශ්නය : ඔබ අධ්යාපනික ග්රන්ථ කියැවීමට කැමති ද?
පිළිතුර පිළිතුරු ගණන (සංඛ්යාතය ƒ)
ඔව් 20
නැත 60
(N)=80
ලැබුණු මුළු පිළිතුරු සංඛ්යාව
2.ඉහත ප්රශ්නයේ ,ඔව්, පිළිතුර ලැබීමේ සංඛ්යාතය (වාර ගණන)——— කි.
20
- 1 වන උදාහරණය ස`දහා පිළිතුරු සැපයූ මුළු නියැදිය 80කි. ඉන් ———පිළිතුරු ‘ඔව්’ සහ——— පිළිතුරු ‘නැත’ විය.
20
60
- ඒ අනුව 1 වන උදාහරණයෙහි 20 සහ 60 යනු —————————– වේ.
(frequencies)
- 1 වන උදාහරණයෙහි ‘ඔව්’ සහ ‘නැත’ යනු——————————— වේ.
(categories)
- අභිශුන්ය කල්පිතය :බමකක යහචදඑයැිසි* යනු 1 වන උදාහරණයෙහි සඳහන් ප්රශ්නයට,‘ඔව්’ සහ ‘නැත’ යන පිළිතුරු ලැබීමේ සංඛ්යාත අතර වෙනසක් ———— යනුයි.
නැත
- ඔව්’ සහ ‘නැත’ යන පිළිතුරු ලැබීමේ සංඛ්යාත අතර වෙනසක් නැති නම්, එකී එක් එක් කාණ්ඩය ස`දහා
———-ක පිළිතුරු ප්රමාණයක් අපේක්ෂා කළ හැකි ය.
50%
- ‘ඔව්’ යන පිළිතුර ලැබීමේ අපේක්ෂිත අගය 50% නම්, ‘ඔව්’ පිළිතුර ස`දහා අපේක්ෂිත සංඛ්යාතය ———–වේ. ඊට හේතුව ශිෂ්ය නියැදිය 80 නිසා එයින් 50%ක් වීම ය.
40
අප දැන් කයිවර්ග පරීක්ෂාව ගණනය කරන අයුරු සහ එය ගණනය කිරීමට භාවිත කරන සූත්රය හඳුනා ගනිමු.
කයිවර්ග පරීක්ෂාව ගණනය කරන අයුරු

උක්ත උදාහරණයේ ආපතිකතා වගුව යනු

- නිරීක්ෂිත සංඛ්යාතය අපේක්ෂිත සංඛ්යාතයෙන් වෙනස් වන අවස්ථාවල දී, මෙසේ ඇති ව තිබෙන වෙනස වෙසෙසි දැයි පරීක්ෂා කිරීමට යොදා ගනු ලබන පරික්ෂාව———- පරික්ෂාව වේ.
කයි වර්ග
- ………….. යනු කයි වර්ග පරික්ෂාව ස`දහා යොදා ගනු ලබන ශ්රිත සංකේතය වේ.
X2
- |o-E|-05 යනුවෙන් අදහස් වන්නේ ,එක් එක් කාණ්ඩ ස`දහානිරීක්ෂිත සංඛ්යාතය සහ අපේක්ෂිත සංඛ්යාතය අතර වෙනසේ අගයෙන් (absolute) ————– ක් අඩු කරන්න, යන්න ය.
0.5
- |o-E|-05 මෙලෙස 0.5 ක් අඩු කිරීමේ සංසිද්ධිය —————– නිරවද්යතාව යනුවෙන් හැදින්වේ.
යේට්ස් (Yates)
මෙසේ යේට්ස් නිරවද්යතාව කරනුයේ සුචලන අංකය 1ක් පමණක් වන ආපතිකතා වගුවකට සන්තතිකතාව සඳහා වන යේට්ස් ශෝධනය නමින් හැදින්වෙන ශොධනයක් භාවිත කරයි.
- (|O-E|-0.5)2/E මින් අදහස් වන්නේ නිරීක්ෂිත සංඛ්යාතය සහ අපේක්ෂිත සංඛ්යාතය අතර වෙනසේ අගයෙන් යේට්ස් නිරවද්යතාව අඩු කර එහි ————- ගණනය කර එය ———————————– බෙදිය යුතු බවයි.
වර්ගය , අපේක්ෂිත සංඛ්යාතයෙන්
14.∑ යන සංකේතයෙන් දැක්වෙනුයේ X2 පරීක්ෂාව සඳහා අදාළ සිද්ධියේ සියලූ කාණ්ඩවල ————— ගන්නා බවයි. එමගින් කරනුයේ අදාළ සිද්ධියට භාජනය වන සියලූ ම කාණ්ඩවල අපේක්ෂිත සහ නිරීක්ෂිත සංඛ්යාත අතර වෙනස (ආපතිකතා වගුවකට සන්තතිකතාව) ඵෙක්යයක් ලෙස ගැනීමයි.
ඵෙක්යයක්
ආපතිකතා වගුවක් යනු- වස්තු කිහිපයක් වර්ගීකරණය කිරීමේ දී අනුමාන 2 කට අනුව වර්ගීකරණය කොට සකස් කරන වගුව ආපකිතතා වගුවක් වේ.
- ඒ අනුව 1 වන උදාහරණයෙහි “ඔව්” සහ”නැත” යන කාණ්ඩ දෙක සැලකීමෙන්
=9.5 + 9.5
=19
මෙතෙක් සාකච්ඡ කළ කරුණු අනුව පැහැදිලි වන්නේ කයි වර්ග පරීක්ෂාව ගණනය කිරීමේ දී, එක් එක් පන්තිය හෙවත් පේළියට (මෙහි දී පේළි දෙකක) අයත් නිරීක්ෂිත හා අපේක්ෂිත අගයයන් අතර වෙනසත් එම වෙනසෙහි වර්ගයත් සෙවිය යුතු බවයි. ඉන් පසු එසේ ලැබෙන අගය, ඒ ඒ පන්තියට අයත් අපේක්ෂිත අගයෙන් බෙදිය යුතු බවයි. අනතුරු ව එම අගයයන් සියල්ල එකතු කළ යුතු ය.
- කෝෂ (cells) යනු අපේක්ෂිත සංඛ්යාත ලැබීම සඳහා ඇති —————- වේ.
කාණ්ඩ
- ඉහත උදාහරණයට කෝෂ ————— ඇත.
02
- උදාහරණය සඳහා කෝෂ 02ක් ඇත. ඒවා ———— සහ ———– කාණ්ඩ වේ.
ඔව්, නැත
- සුචලන අංකය (df) තීරණය කිරීම හෙවත් df යනු කෙතරම් කෝෂ (cells) ගණනක සංඛ්යාත ———— වීමට ඉඩකඩක් ඇති ද යනුයි.
වෙනස්
- උදාහරණයෙහි ”ඔව්” ලැබීෙමි සංඛ්යාතය දන්නේ නම් “නැත” ලැබීමේ සංඛ්යාතය ————— වේ. මෙහි වෙනස් වීමට ඇත්තේ කෝෂ 2ක් පමණි.
ස්ථාවර
- මන්ද මෙහි මුළු සංඛ්යාතය 80 වේ. එනම් මෙහි එක් (cell) කෝෂයකට පමණක් වෙනස් වීමේි නිදහස ඇත.
එනම් df = ————- කි.
01
- දැන් ඉහත උදාහරණයෙහි සුචලන වගු භාවිතයෙන් අගය ලබා ගන්නා ආකාරය ඉගෙන ගනිමු. සුචලන වගුව පහත දැක්වේ.
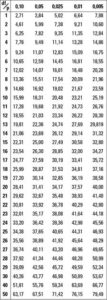
වෙසෙසියා මට්ටම (Significance level) යන සංකල්පය මෙහි දී තේරුම් ගැනීම වැදගත් ය.
(සාමාන්යයෙන් පර්යේෂණවල දී භාවිත කෙරෙන වෙසෙසියා මට්ටම් 2ක් පවතියි. එනම් 0.05 (5%) සහ 0.01 (1%) වේ. 0.05 (5%) මට්ටමේ දී, පර්යේෂක ගනු ලබන තීරණය නිවැරදි වීමට, 95%ක හැකියාවක් ඇත. එය වැරදි තීරණයක් වීමට 5%ක හැකියාවක් පවති.0.01 (1%) මට්ටමේ දී, පර්යේෂක ගනු ලබන තීරණය නිවැරදි වීමට, 99%ක හැකියාවක් ඇත. එය වැරදි තීරණයක් වීමට 1%ක හැකියාවක් පවති. වෙනත් පදවලින් කිව හොත් ,අපේක්ෂිත සහ නිරීක්ෂිත අගය අතර වෙසෙසි වෙනසක් නොපවති, යන කල්පිතය සත්ය වන විට එය ප්රතික්ෂේප කිරීමට, එනම් වැරදි තීරණයක් ගැනීමට 0.05 (5%) හෝ 0.01 (1%) ඉඩක් ඇත).
මෙහි දී අපි 0.01 යොදා ගනිමු. ඒ අනුව df = 1 දී හා වෙසෙසියා මට්ටම 0.01 දී
X2වගු අගය = 6.64 වේ. (වගුවේ මෙය සඳහන් අයුරු බලන්න. මෙය අවධි අගය ලෙස ද හදුන්වය)
- නිගමනය ලබා ගැනීම.
X22ගණනය අගය > X22වගු අගය
19 > 6.64
ඒ අනුව උදාහරණයෙහි කාණ්ඩ දෙක අතර සංඛ්යාතවල වෙනස ————— වෙසෙසියා මට්ටමක දී වෙසෙසි වේ. ඒ අනුව අභිශූන්ය කල්පිතය ප්රතික්ෂේප කරයි. එනම් තෝරා ගත් නියැදියේ බොහෝ පිරිසක් අධ්යාපනික ග්රන්ථ කියවීම ප්රතික්ෂේප කරති.
0.01
ගයානි පන්නල
සංඛ්යාන විද්යා සම්බන්ධීකරණ නිලධාරිණි
