පර්යේෂණ දත්ත විශ්ලේෂණය සඳහා සංඛ්යාන විද්යාව
කයි වර්ග පරීක්ෂාව (Chi squared test)
සංඛ්යාන විද්යාව පිළිබඳ මේ ලිපි මාලාව ලිවීමේ දී බී. එෆ්. ස්කිනර් විසින් හදුන්වා දුන් පියවර පාඩම් ක්රමය (Programmed learning) ද භාවිත කරනු ලැබේ. එහි දී ඔබේ ඉගෙනුම් පහසුව තකා හිස්තැන් පිරවීමේ ප්රශ්න සහ එම ප්රශ්නවලට පිළිතුරු ලිපියට ඇතුළත් කර ඇත. මෙම ලිපි මාලාවේ පළමු හා දෙ වන කොටස් පසුගිය කලාපවල පළ වූ අතර, මේ එහි තෙවැන්නයි.
පර්යේෂණයක දී දත්ත රැස් කරන විට ලැබෙන අගයයන් සහ එම පර්යේෂණයේ දී පර්යේෂක බලාපොරොත්තු වන අගයයන් අතර වෙනසක් තිබෙන්නට පුළුවන. එම වෙනස අහම්බෙන් වූ වෙනසක් ද නැත හොත් වෙසෙසි වෙනසක් ද යන්න නිශ්චය කර ගැනීමට කරනු ලබන පරීක්ෂාව කයි වර්ග පරීක්ෂාව (Chi squared test) යනුවෙන් හැදින්වේ.
කයි වර්ග පරීක්ෂාව ප්රධාන අවස්ථා 2ක දී සිදු කරයි.
ඒකීය නියැදි (Single sample) බහු නියැදි (Multiple samples)
ඒකීය නියැදි සදහා යොදා ගන්නා කයි වර්ග පරීක්ෂාව සුචලන අගය මත ආකාර 2කි.
සුචලන අංකය 1 වන විට (df=1) (ගවේෂණ 27 කලාපයේ දී පැහැදිලි කෙරිණි)
සුචලන අංකය 1ට වඩා වැඩි විට (df>1) (ගවේෂණ 28 කලාපයේ දී පැහැදිලි කෙරිණි)
පෙර ලිපිවලින් සාකච්ඡ කරන ලද්දේ ඒකීය නියැදි පදනම් කර ගත් පර්යේෂණවලින් ලද දත්ත විශ්ලේෂණය සඳහා කයි වර්ග පරීක්ෂාව යොදා ගන්නා ආකාරය ගැනයි. පර්යේෂකයකු හට බහු නියැදි (එකකට වැඩි නියැදි සංඛ්යාවක) පාදක පර්යේෂණවලින් ලැබෙන දත්ත සඳහා ද කයි වර්ග පරීක්ෂාව භාවිත කළ හැකි ය. එනම් පර්යේෂණවල දී විවිධ වූ නියැදි කාණ්ඩ පවතින විට, එම විවිධ නියැදි කාණ්ඩවලින් ලැබුණු අගයයන් (Observed frequencies) සහ බලාපොරොත්තු වූ අගයයන් (Expected frequencies) අතර වෙනසක් තිබිය හැකි දැයි සෙවීමට ද කයි වර්ග පරීක්ෂාව භාවිත කළ හැකි ය. වෙනසක් වේ නම්, එම වෙනස අහම්බෙන් වූ වෙනසක් ද නැත හොත් වෙසෙසි වෙනසක් ද යන්න නිශ්චය කර ගැනීමට කයි වර්ග පරීක්ෂාව යොදා ගනු ලැබේ. දැන් අපි උදාහරණයක් ඇසුරින් මේ පිළිබඳ ව විමසා බලමු.
උදා:- එක්තරා පාසලක ඉගෙනුම ලබන ගැහැනු සහ පිරිමි ළමයින්ගේ ශාස්ත්රීය සංගීතය සදහා ඇති කැමැත්ත විමසීමට පර්යේෂණයක් කළ අතර, ඒ සදහා විමසූ පිළිතුරු 3ක් සහිත ප්රශ්නයකට ශිෂ්ය ශිෂ්යාවන් ලබා දුන් ප්රතිචාර ගණන් (සංඛ්යාත) 1 වන වගුවේ දැක්වේ.
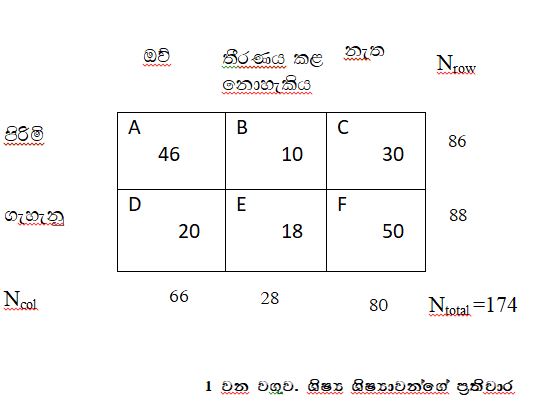
1. 1 වන වගුවේ උදාහරණයේ පිළිතුරු කාණ්ඩ 3ක් (ඔව්-තීරණය කළ නො හැකි ය-නැත) දැක්වෙන අතර එම පිළිතුරු කණ්ඩායම් …….ක් විසින් ලබා දී ඇත.
2
2. ගැහැනු ළමයින් කණ්ඩායමක් සහ පිරිමි ළමයින් කණ්ඩායමක් සමීක්ෂණයට සහභාගි වූ නිසා කණ්ඩායම් දෙකකි. එම කණ්ඩායම් දෙකේ වූ මුළු ළමයින් සංඛ්යාව (N total )= …….. වේ.
174
3. පිරිමි ළමයින් සංඛ්යාව 86කි. එය Nrow ලෙස ඉහත වගුවේ දක්වා ඇත. එනම් ඉහළ පේළියේ (Cells) කාණ්ඩ 03හි එකතුව වේ (Cell A,B සහ C). ගැහැනු ළමයින් සංඛ්යාව …….. කි. එනම් …….. (Cells) පේළියේ කාණ්ඩ 3හි එකතුව වේ (Cell D, E සහ F).
88, පහළ
4. මෙම සමීක්ෂණයට සහභාගි වූ ළමයින් 174 අතුරින් 66 දෙනකු “ඔව්” යන පිළිතුර ද (පළමු තීරයේ එකතුව) 28 දෙනකු “තීරණය කළ නොහැකිය” යන පිළිතුර ද (දෙ වන තීරයේ එකතුව) සහ …….. දෙනකු “නැත” යන පිළිතුර ද (තෙ වන තීරයේ එකතුව) ලබා දී ඇත.
80
5. පිරිමි ළමයින් 86 අතුරෙන් 46 දෙනකු “ඔව්” යනුවෙන් ද (Cell A); 10 දෙනකු “තීරණය කළ නොහැකිය” යන පිළිතුර ද (Cell B); …….. දෙනකු “නැත” යන පිළිතුර ද (Cell C) ලබා දී ඇත.
30
6. මේ පර්යේෂණයේ අභිශූන්ය කල්පිතය (H0): ගැහැනු සහ පිරිමි ළමයින් ලබා දුන් පිළිතුරුවල වෙනසක් නැත.
පර්යේෂණයේ දී ලබා දීමට තිබූ පිළිතුරෙහි කාණ්ඩ 3කි (ඔව් – තීරණය කළ නො හැකි ය – නැත වසයෙනි). පිළිතුරු දීමට සිටි කණ්ඩායම් ගණන 2කි (ගැහැනු – පිරිමි වසයෙනි).
ඒ අනුව පර්යේෂණයේ දී ලබා දුන් ප්රතිචාර, සංඛ්යාත කෝෂ (Cell) ……..ට බෙදා දැක්වෙයි.
6
7. කයි වර්ග පරීක්ෂාව මගින් සොයා බලනුයේ පිරිමි ළමයින් ලබා දුන් පිළිතුරු සංඛ්යාත ……………. ……………. ලබා දුන් පිළිතුරු ……………. අතර වෙනස, වෙසෙසි වෙනසක් ද යන්නයි.
ගැහැනු ළමයින් , සංඛ්යාත
8. 1 වන වගුවෙන් එක් එක් කාණ්ඩ සදහා නිරීක්ෂිත සංඛ්යාත කෝෂ 06ක් මගින් දක්වා ඇත. ඒ අනුව කයි වර්ග (X2) පරීක්ෂාව සිදු කිරීමට එක් එක් කෝෂ (Cell) සදහා ……………. සංඛ්යාත සෙවිය යුතු වේ. ඒ සඳහා 1 වන වගුවේ සඳහන් සූත්රය භාවිත කළ හැකි ය.
අපේක්ෂිත

9. දැන් අපි කෝෂය A (Cell A) සදහා අපේක්ෂිත සංඛ්යාතය (E) සොයමු. ඒ සදහා Nrow (එනම් කෝෂය A පිහිටි පේළියේ මුළු සංඛ්යාතය) සෙවිය යුතු ය. Nrow = …….. (46+10+30)
86
10. දැන් Ncol සොයමු. එනම් කෝෂය A පිහිටි තීරයේ මුළු සංඛ්යාතයි. Ncol = …….. (46+20)
66
11. 2 වන සූත්රය යොදා ගනිමින් එක් එක් කෝෂ (Cell) සදහා අපේක්ෂිත සංඛ්යාත සොයමු.
කෝෂය A සදහා අපේක්ෂිත සංඛ්යාතය
E = (86) (66)/ 174
= 32.6
කෝෂය B සදහා අපේක්ෂිත සංඛ්යාතය
E = (86) (28)/174
=13.8
කෝෂය C සදහා අපේක්ෂිත සංඛ්යාතය
E = (86) (80)/174
= 39.5
කෝෂය D සදහා අපේක්ෂිත සංඛ්යාත
E = (88) (66)/174
= 33.4
කෝෂය E සදහා අපේක්ෂිත සංඛ්යාතය
E = (88) (28)/174
= 14.2
කෝෂය F සදහා අපේක්ෂිත සංඛ්යාතය
E = (88) (80)/174
= 40.5
ඒ අනුව අපේක්ෂිත සංඛ්යාත 3 වන වගුවෙන් දැක්වෙයි
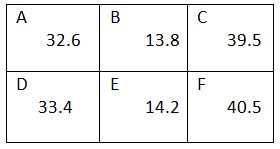
12. ඒ අනුව කෝෂය D සදහා නිරීක්ෂිත සංඛ්යාතය 0=…….. හා අපේක්ෂිත සංඛ්යාතය E =…….. .
20, 33.4
13. දැන් අපි කෝෂය A සදහා වන කයි වර්ග පරීක්ෂාව සෙවීම සඳහා 2 වන සූත්රය භාවිත කරමු.
ඒ සදහා සුචලන අංකය (df) සොයමු
1 වන සූත්රයෙහි සදහන්
(සුචලන අංකය (df) = (පේළි ගණන – 1) (තිර ගණන – 1)
යන්න පරිදි සුචලන අංකය (df) = :2-1) (3-1) = 2 වෙයි.
ඒ අනුව (df) 2 වන විට අප X2 පරීක්ෂාව සදහා යොදා ගනු ලබන පහත සඳහන් 2 වන සූත්රය (මේ පිළිබඳ ව වැඩිපුර විස්තර ‘ගවේෂණ’ පසුගිය කලාපය මගින් ඉදිරිපත් කරන ලදී) මෙහි දි භාවිත කරනු ලැබේ.
2 වන සූත්රය
X2 = (0-E)2/E
ඒ අනුව කෝෂය A සදහා χ2 පරීක්ෂාව පහත සඳහන් පරිදි වේ.
(0-E) = …….., (0-E)2 = …….., (0-E)2 = ……../E,
14. ඉතිරි කෝෂ සදහා X2 පරීක්ෂාව
B = …….. C = …….. D = …….. E = …….. F = ……..
15. මේ අනුව සූත්රය 2 යොදමු
1.04, 2.28, 5.37, 1.01, 2.23
= ……..
17.44
16. සුචලන අංකය df ගණනය කිරීම
df = (පේළි ගණන – 1) (තීර ගණන – 1)
= (2-1) (3-1)
= ……..
2
17. සුචලන අංකය යනු කෙතරම් කෝෂ (Cell) ගණනක සංඛ්යාත වෙනස් වීමට ඉඩකඩක් ඇති ද යනුයි.
සුචලන අංකය (df) = 2 එනම් කෝෂ 2ක සංඛ්යාත වෙනස් වීමට ඉඩකඩක් ඇත.
මෙහි මුළු කෝෂ ගණන 06කි. ඒ අනුව මේ උදාහරණයේ Ntotal = 174 හි කෝෂ ……..ක සංඛ්යාත ස්ථාවර වේ
4
18. X2 = 17.44 සහ df = 2
මෙහි 17.44 යනු ගණනය කිරීම් මගින් ලබා ගත් කයි වර්ගයේ අගයයි.
දැන් අපි සුචලන වගු භාවිතයෙන් 0.05 වෙසෙසියා මට්ටමක දී X2වගු අගය ලබා ගනිමු. මේ සදහා සුචලන වගුව භාවිත කරනු ලැබේ.
ඒ අනුව 0.05 වෙසෙසියා මට්ටමේ දී …….. ද 0.01 වෙසෙසියා මට්ටමේ දී …….. වේ.
5.99, 9.21
වෙසෙසියා මට්ටම (Significance level)
සාමාන්යයෙන් පර්යේෂණවල දී භාවිත කෙරෙන වෙසෙසියා මට්ටම් 2ක් පවතියි. එනම් 0.05 (5%) සහ 0.01 (1%) වේ. එනම් 5 (5%) මට්ටමේ දී, පර්යේෂක ගනු ලබන තීරණය නිවැරදි වීමට, 95%ක හැකියාවක් ඇත. එය වැරදි තීරණයක් වීමට 5%ක හැකියාවක් පවතී. 0.01 (1%) මට්ටමේ දී, පර්යේෂක ගනු ලබන තීරණය නිවැරදි වීමට, 99%ක හැකියාවක් ඇත. එය වැරදි තීරණයක් වීමට 1%ක හැකියාවක් පවතී. වෙනත් පදවලින් කිව හොත් (අපේක්ෂිත සහ නිරීක්ෂිත අගය අතර, වෙසෙසි වෙනසක් නොපවතී” යන කල්පිතය සත්ය වන විට එය ප්රතික්ශේප කිරීමට, එනම් වැරදි තීරණයක් ගැනීමට 0.05% (5%) හෝ 0.01 (1%) ඉඩක් ඇත.
19. නිගමනය ලබා ගැනීම
X2 ගණනය අගය > X2 වගු අගය
17.44 > 5.99
එනම් 0.05 වෙසෙසියා මට්ටමේ දී කාණ්ඩ අතර සංඛ්යාතවල වෙනස …….. වේ
වෙසෙසි
20. එනම් ඉහත උදාහරණයේ අභිශූනය කල්පිතය …….. කරයි. එනම් ගැහැනු සහ පිරිමි කාණ්ඩ දෙන ලද පිළිතුරු කාණ්ඩවල සංඛ්යාත අතර වෙනසක් නැත යන්න ප්රතික්ෂේප කරයි.
ප්රතික්ෂේප
ගයානි පන්නල
සංඛ්යාන විද්යා සම්බන්ධීකරණ නිලධාරිණි
පර්යේෂණ හා සංවර්ධන ආයතනය
